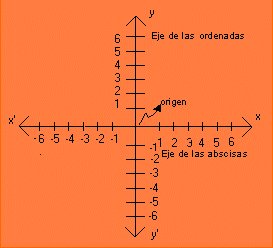
El Plano Cartesiano está formado por dos rectas numéricas,
una horizontal y otra vertical que se cortan en un punto. La recta horizontal
es llamada eje de las abscisas o de las equis (x), y la vertical, eje de las
ordenadas o de las yes, (y); el punto donde se cortan recibe el nombre de
origen.
El plano cartesiano tiene como finalidad describir la
posición de puntos, los cuales se representan por sus coordenadas o pares
ordenados. Las coordenadas se forman asociando un valor del eje de las
"X" y uno de las "Y", respectivamente, esto indica que un
punto se puede ubicar en el plano cartesiano con base en sus coordenadas, lo
cual se representa como:
Para localizar puntos en el plano cartesiano se debe llevar
a cabo el siguiente procedimiento:
1. Para localizar la abscisa o valor de x, se cuentan las
unidades correspondientes hacia la derecha si son positivas o hacia a izquierda
si son negativas, a partir del punto de origen, en este caso el cero.
2. Desde donde se localiza el valor de x, se cuentan las
unidades correspondientes hacia arriba si son positivas o hacia abajo, si son
negativas y de esta forma se localiza cualquier punto dadas sus coordenadas.
Ejemplos:
Localizar el punto A ( -4, 5 ) en el plano cartesiano. Este
procedimiento también se emplea cuando se requiere determinar las coordenadas
de cualquier punto que esté en el plano cartesiano.
Determinar las coordenadas del punto M.
Las coordenadas del punto M son (3,-5).
Las coordenadas del punto M son (3,-5).
Ejemplos Audiovisuales de la ubicación de coordenada o putos en el plano cartesiano
Traslaciones en el Plano Cartesiano
La traslación es
una transformación isométrica, la figura u objeto conserva sus
medidas, al cual se le aplica un vector. Explicado de la forma más simple
posible, éste vector indica el movimiento de la figura u objeto en el plano
cartesiano.
Ejemplo: Audiovisual de Traslación en el Plano

No hay comentarios:
Publicar un comentario